Notación proposicional de la probabilidad

• P(A): probabilidad incondicional de que A sea cierto. Debe usarse sólo cuando no hay más información
• variables aleatorias: variables que tienen probalibidades de tener distintos valores
  • P(Weather=Sunny)=0.7, P(Weather=Rain)=0.2,
    P(Weather=Cloudy)=0.08, P(Weather=Snow)=0.02,
  • Cada variable aleatoria tiene un dominio x1, ..., xn de posibles valores (en principio discretos). Los símbolos proposicionales pueden considerarse como variables aleatorias con dominio true, false. (Notación: A, B, ... para variables aleatorias booleanas; X, Y, ... para variables aleatorias multivaluadas)
  • P(Weather) denota todas las probabilidades de todos los posibles valores de la variable aleatoria Weather
  • distribución de probabilidad para la variable aleatoria Weather:
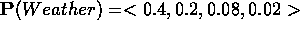
  • P(Weather, Cavity) denota las probabilidades de todas las combinaciones de valores de esas dos variables (en este caso una tabla 4 por 2 de probabilidades)
• probabilidad condicional: se usa cuando se ha obtenido alguna evidencia
• la probabilidad de A dado que todo lo que conocemos es B: probabilidad de A condicionado a B
• tan pronto conozcamos C, debemos computar
• 
• es una tabla de dos dimensiones que nos da las para cada posible valor i, j
• la probabilidad condicional se pueden obtener a partir de las probabilidades a priori: siempre que P(B)>0
  la ecuación puede reescribirse como la regla del producto:
  o también
  
• denota un conjunto de ecuaciones que se corresponden con las entradas individuales de la tabla; una de esas ecuaciones:
• no significa siempre que B sea cierto, concluir A con P(A)=0.8, obsérvese que
  • P(A) siempre denota la probabilidad a priori, no la probabilidad a posteriori dada alguna evidencia
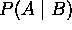  • sólo es aplicabe cuando B es la única evidencia disponible