


Next: Inferencia en redes de
Up: Inferencia en redes de
Previous: Tipos de inferencias probabilísticas
- algoritmo para poliárboles: redes en las que como máximo hay un camino no dirigido entre cualesquiera dos nodos de la red
- soporte causal
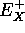 : las variables de evidencia por encima de X que están conectadas a X a través de sus padres
: las variables de evidencia por encima de X que están conectadas a X a través de sus padres - soporte evidencial
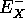 : las variables de evidencia por debajo de X que están conectadas a X a través de sus hijos
: las variables de evidencia por debajo de X que están conectadas a X a través de sus hijos -
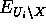 : denota toda la evidencia conectada al nodo Ui excepto por el camino de X
: denota toda la evidencia conectada al nodo Ui excepto por el camino de X - estrategia general para el cálculo de
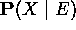
- expresar
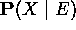 en términos de la contribución de
en términos de la contribución de 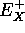 y
y 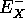
- obtener
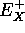 , calculando el efecto en los padres de X y pasando luego el efecto a X (recursivo)
, calculando el efecto en los padres de X y pasando luego el efecto a X (recursivo) - obtener
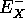 , calculando el efecto en los hijos de X y pasando luego el efecto a X (recursivo)
, calculando el efecto en los hijos de X y pasando luego el efecto a X (recursivo)
-
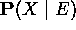 , cálculo en detalle
, cálculo en detalle
-
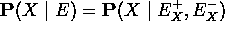
- para separar
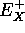 y
y 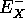 aplicamos la versión condicional de la regla de Bayes manteniendo
aplicamos la versión condicional de la regla de Bayes manteniendo 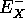 como evidencia de fondo
como evidencia de fondo
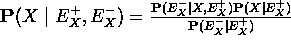
- ya que X separa-d
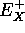 de
de 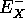 , usamos independencia condicional para simplificar el primer término del numerador. También tratamos
, usamos independencia condicional para simplificar el primer término del numerador. También tratamos 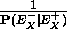 como una constante de normalización, por tanto
como una constante de normalización, por tanto
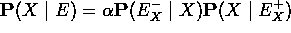
- cálculo de
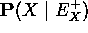
- Sea U=U1, ..., Um el vector de padres de X y u una asignación de variables a este vector, entonces
- ya que U separa-d X de
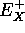 podemos simplificar el primer término a
podemos simplificar el primer término a 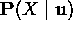 . Debido a que
. Debido a que 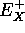 separa-d cada uno de los Ui de los demás y teniendo en cuenta que la probabilidad de una conjunción de variables independientes es igual al producto de sus probabilidades individuales
separa-d cada uno de los Ui de los demás y teniendo en cuenta que la probabilidad de una conjunción de variables independientes es igual al producto de sus probabilidades individuales
- el último término se puede simplificar particionando
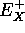 en
en 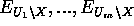 y teniendo en cuenta que
y teniendo en cuenta que 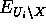 separa-d
separa-d 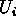 del resto de evidencia en
del resto de evidencia en 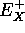 , por tanto
, por tanto
- volviendo a la ecuación original
esta expresión es adecuada para el algoritmo que buscamos ya que
-
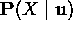 se obtiene en la tabla de probabilidad condicional de X
se obtiene en la tabla de probabilidad condicional de X -
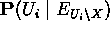 es un caso recursivo del problema original, que era
es un caso recursivo del problema original, que era 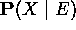 , es decir
, es decir 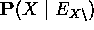
- obsérvese que el conjunto de variables de la llamada recursiva es un subconjunto de las de la llamada original
- cálculo de
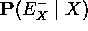
- sean Zi los padres de Yi distintos de X y zi una asignación de valores a esas variables. Ya que la evidencia en cada Yi es condicionalmente independiente de los otros (dado X), tenemos que
- promediando sobre Yi y zi
- dividiendo
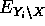 en dos componentes independientes
en dos componentes independientes 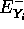 y
y 
-
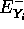 es independiente de X y zi (dado yi)
es independiente de X y zi (dado yi)
 es independiente de X y de yi, y además sacando los términos sin zi fuera del sumatorio de zi
es independiente de X y de yi, y además sacando los términos sin zi fuera del sumatorio de zi
- aplicando la regla de Bayes a
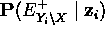
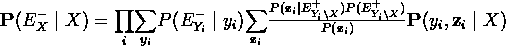
- reescribiendo la conjunción Yi, zi
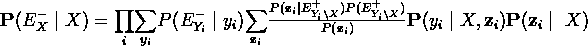
- ya que Z y X están d-separados,
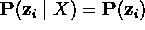 , con lo que se cancelan. Además reemplazamos
, con lo que se cancelan. Además reemplazamos 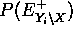 por una constante de normlización
por una constante de normlización 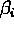
- finalmente los padres de los Yi (los Zij) son independientes entre si por lo que pueden multiplicarse como se hizo antes con los Ui. Además se combinan los
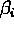 en una constante de normalización
en una constante de normalización 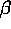
esta es una expresión adecuada para el algoritmo ya que
-
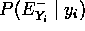 es un caso recursivo de
es un caso recursivo de 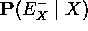
-
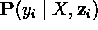 es una entrada de la tabla de probabilidad condicional para Yi
es una entrada de la tabla de probabilidad condicional para Yi -
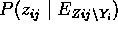 es un caso recursivo de
es un caso recursivo de 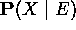 (es decir
(es decir 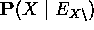 )
)
- detalles del algoritmo
- SUPPORT-EXCEPT(X, V) calcula
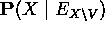 que es una generalización de 4d para tratar la variable de excepción V
que es una generalización de 4d para tratar la variable de excepción V - EVIDENCE-EXCEPT(X, V) calcula
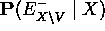 que es una generalización de 5h
que es una generalización de 5h - el algoritmo hace llamadas recursivas desde X a través de tods los caminos de la red. La recursividad termina en los nodos evidencia, nodos raíces y nodos hoja. La llamada recursiva excluye el nodo desde el que se hace con lo que cada nodo se visita sólo una vez
- el algoritmo sólo funciona en poliárboles. Si hubiese más de un camino entre un par de nodos, la recursividad contaría la misma evidencia más de una vez o no terminaría correctamente
- el algoritmo es de encadenamiento hacia atrás. Desventaja: el algoritmo calcula la distribución de probablilidad sólo para una variable. Para calcularla para todas las variables pregunta habría que ejecutar el algoritmo una vez para cada una (coste en tiempo cuadrático)
- existen algoritmos para propagar la evidencia hacia delante mediante paso de mensajes



Next: Inferencia en redes de
Up: Inferencia en redes de
Previous: Tipos de inferencias probabilísticas
Alvaro Barreiro Garcia
Tue Jul 23 18:15:28 MET DST 1996
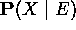 en términos de la contribución de
en términos de la contribución de 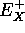 y
y 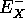
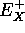 , calculando el efecto en los padres de X y pasando luego el efecto a X (recursivo)
, calculando el efecto en los padres de X y pasando luego el efecto a X (recursivo) 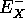 , calculando el efecto en los hijos de X y pasando luego el efecto a X (recursivo)
, calculando el efecto en los hijos de X y pasando luego el efecto a X (recursivo)
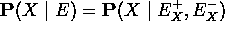
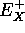 y
y 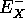 aplicamos la versión condicional de la regla de Bayes manteniendo
aplicamos la versión condicional de la regla de Bayes manteniendo 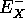 como evidencia de fondo
como evidencia de fondo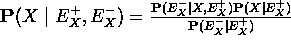
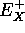 de
de 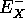 , usamos independencia condicional para simplificar el primer término del numerador. También tratamos
, usamos independencia condicional para simplificar el primer término del numerador. También tratamos 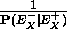 como una constante de normalización, por tanto
como una constante de normalización, por tanto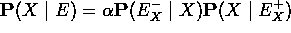
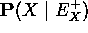
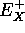 podemos simplificar el primer término a
podemos simplificar el primer término a 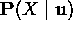 . Debido a que
. Debido a que 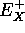 separa-d cada uno de los Ui de los demás y teniendo en cuenta que la probabilidad de una conjunción de variables independientes es igual al producto de sus probabilidades individuales
separa-d cada uno de los Ui de los demás y teniendo en cuenta que la probabilidad de una conjunción de variables independientes es igual al producto de sus probabilidades individuales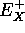 en
en 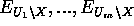 y teniendo en cuenta que
y teniendo en cuenta que 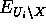 separa-d
separa-d 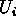 del resto de evidencia en
del resto de evidencia en 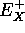 , por tanto
, por tanto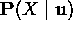 se obtiene en la tabla de probabilidad condicional de X
se obtiene en la tabla de probabilidad condicional de X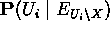 es un caso recursivo del problema original, que era
es un caso recursivo del problema original, que era 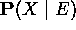 , es decir
, es decir 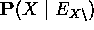
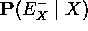
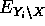 en dos componentes independientes
en dos componentes independientes 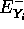 y
y 
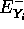 es independiente de X y zi (dado yi)
es independiente de X y zi (dado yi)
 es independiente de X y de yi, y además sacando los términos sin zi fuera del sumatorio de zi
es independiente de X y de yi, y además sacando los términos sin zi fuera del sumatorio de zi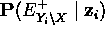
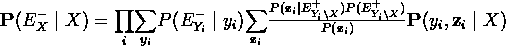
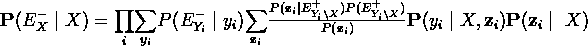
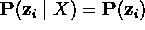 , con lo que se cancelan. Además reemplazamos
, con lo que se cancelan. Además reemplazamos 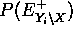 por una constante de normlización
por una constante de normlización 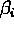
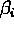 en una constante de normalización
en una constante de normalización 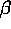
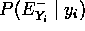 es un caso recursivo de
es un caso recursivo de 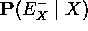
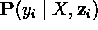 es una entrada de la tabla de probabilidad condicional para Yi
es una entrada de la tabla de probabilidad condicional para Yi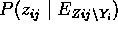 es un caso recursivo de
es un caso recursivo de 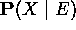 (es decir
(es decir 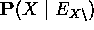 )
)
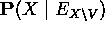 que es una generalización de 4d para tratar la variable de excepción V
que es una generalización de 4d para tratar la variable de excepción V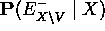 que es una generalización de 5h
que es una generalización de 5h