VVS: model checking
Petri Nets
Introduction
In this exercise we will use SPIN to
verify properties about Petri
Nets, a kind of transition graph commonly used for
representing concurrent protocols involving shared
resources in many areas in Computer Science such as
Concurrent Programming, Software Engineering, Workflow
modeling, Simulation, Diagnosis or Business Process
Modeling. They can be used, for instance, as an
alternative to Activity Diagrams in UML.
Definitions: a Petri Net is a graph formed by two disjoint sets of nodes, T and P, respectively called transitions (represented as thick bars) and places (depicted as circles), and a set of arcs A ⊆ (T x P) ∪ (P x T). This means that arcs can go from a place to a transition or vice versa, but will never connect two places or two transitions directly. Given a transition t, we define its incoming places as In(t) := {p | (p,t) ∈ A} and its outgoing places as Out(t) := {p | (t,p) ∈ A}. A marking M of the net is a function M: P -> Nat assigining a natural number to each place in the net. Graphically, if M(p)>0 this is represented by including a number M(p) of black dots (tokens) inside the circle for place p. If M(p)=0 the circle is left empty. A marking is said to be 0-1 if all the places have one or zero tokens. We say that a transition t ∈ T is enabled in a marking M, when M(p)>0 for all input places p ∈ In(t).
Execution: The Petri Net is
executed by defining the valid steps from one marking M
to another M'. A valid step, represented as M
→ M', is such that there exists some enabled
transition t ∈ T in M that has
been fired in M', that is, we have
consumed one token from all input places and produced one
token for all output places. Formally, for any place p,
the value of M'(p) is defined as:
- M(p)-1 if p ∈ In(t) \ Out(t)
- M(p)+1 if p ∈ Out(t) \ In(t)
- M(p) otherwise, that is, p ∈ Out(t) ∩ In(t)
The execution starts from an initial
marking denoted as M0 and
proceeds in consecutive steps M0
→ M1 → M2 →
... As we can see,
executions can run forever: they only stop when there are
no enabled transitions. In a given step, we may have
several enabled transitions so that one is chosen
non-deterministically.
For an easy-to-use tool, including
edition and simulation, try PIPE2.
Goals
The goal of this exercise is playing with a pair of Petri net examples in SPIN and verifying some conditions:- absence of deadlock: we cannot reach a state in which all processes get blocked waiting for something to happen.
- safety: check that a given (wrong)
configuration is not reachable.
- absence of starvation (liveness): check whether some transition is fired infinitely often.
- boundedness: check that the number of tokens in
a given place is bounded.
An elevator is working in a 4 floors building, represented by places P1, P2, P3, P4. The following Petri net represents the possible transitions and the initial situation (the elevator is at the ground floor).
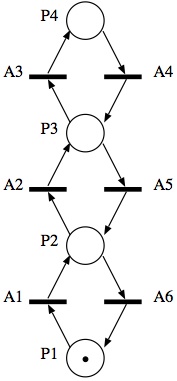
You can try it in PIPE with file elevator.xml. A simple formalization of this problem in Promela can be:
| #define Place byte
// assume at most 255 tokens per place Place p1=1, p2=0, p3=0, p4=0 // place p1 has an initial token #define enabled(x) x>0 -> x-- #define fire(x) x++ active proctype P() { do :: enabled(p1) -> fire(p2); A1: printf("A1\n") :: enabled(p2) -> fire(p3); A2: printf("A2\n") :: enabled(p3) -> fire(p4); A3: printf("A3\n") :: enabled(p4) -> fire(p3); A4: printf("A4\n") :: enabled(p3) -> fire(p2); A5: printf("A5\n") :: enabled(p2) -> fire(p1); A6: printf("A6\n") od } |
Given the initial marking in the picture above, check the following conditions:
- Safety: check whether we could have tokens at two
different floors. Explain the obtained result.
- Fairness: check that each floor is visited infinitely often. Explain the obtained result.
- Boundedness: check that each place in the net is always marked with 0 or 1 tokens, but not more.

This Petri net represents two traffic lights 1 and 2 that can alternate the sequence Green - Orange - Red but should not be Green simultaneously. The Petri net uses one place per each color and traffic light: G1, O1, R1, G2, O2, R2. It contains an additional place S to guarantee that only one green light is turned on. You can try it in PIPE using file traffic.xml. Using the initial marking depicted above:
- Formalize the problem in Promela
- Safety: check that a situation in which both
traffic lights are green is not reachable. Explain
the obtained result.
- Liveness: check whether both traffic lights can reach each color infinitely often. Explain the obtained result.
- Boundedness: check that each place in the net is always marked with 0 or 1 tokens, but not more.
- Use SPIN to check if there exists an initial 0-1 marking that violates the boundedness condition above.
Example 3: Sender and Receiver
In this third example you will have to model the
corresponding Petri net. We have two processes (sender
and receiver) that operate in the following
way:
- When the sender is free, it prepares a new message. Once the message is ready, it sends it to the communication line (a buffer) and keeps waiting for an acknowledgement (ack) from the receiver. When the ack is received, the sender is free to prepare a new message again.
- When the receiver is ready to receive, it waits for some message in the buffer. Once the message is received, it sends an ack signal to the sender and begins processing the received message. When the message has been processed, the receiver becomes ready to receive again.
The buffer has room for a single message, the sender
is initially free and the receiver is initially ready
to receive.
- Design the corresponding Petri Net
- Formalize the problem in Promela
- Check absence of deadlocks
- Liveness: check whether any sent message is
eventually processed by the receiver before we send
anything else
- Check that both sender and receiver may process infinitely often
Assessment & delivery
The deadline for delivery is Friday, December 12th, 2025
(23:59).