Taxi routing

In this exercise, we will use telingo to solve a multiagent planning problem we will call Taxi Routing. It consists in moving a number T of taxis, numbered from 1 to T, to take a number P of passengers, named consecutively with letters a, b, c, etc, to some locations marked as "stations". We may have a different number of passengers and taxis, but the number of stations S is always supposed to be greater or equal than the number of passengers S>=P (otherwise, the problem has no solution). The taxis can move horizontally or vertically through a map that has the form of a rectangular grid possibly containing building cells. These are some additional constraints:

• A taxi cannot drive through a building cell
• Two taxis cannot be at the same time in the same cell
  
• Two persons cannot be at the same time in the same cell. This also forbids simultaneously having, at the same cell, one person inside a taxi and another one outside the taxi
• Two adjacent taxis cannot swap their positions
  

The final goal is to reach a situation where each passenger is outside the taxi at any of the station positions. At each step, a taxi can do one of the following actions:

• move (up, down, left or right)
• pick a passenger (if the taxi is free and there is a person in the same location)
• drop a passenger (if there is one inside the taxi)
• wait
  

What to do

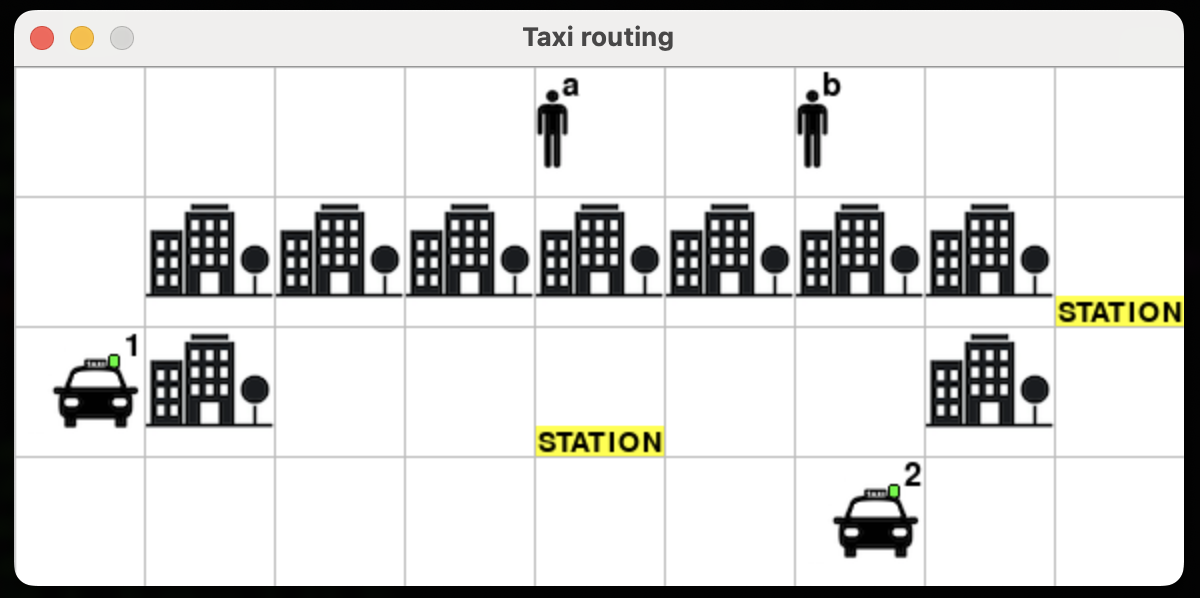
Step 1. Each input instance is an ASCII file containing a rectangular grid with the following format. The file contains n lines (the rows) and each line contains m characters (the columns) ended by a newline. Each cell contains a character that can be:

• . = empty cell
  
• # = a building
• X =  a station
• a,...,z =  a passenger
• 1,...,9 =  a taxi

For simplicity in the input notation, we assume that, initially, all stations are empty, all taxis are free, and all passengers are in a cell without taxi.

The following shows the input format for the initial configuration above, also contained in the example file domain.txt:

....a.b.. .#######X 1#..X..#. ......2..

The file examplestaxi.zip (to be added) contains several input files and their solutions.

Step 2. Write a python program encode.py to transform each input ASCII file into a logic program containing facts. For instance:

python3 encode.py dom01.txt domain.lp

will transform the example above into the set of facts for the predicates you decide to use for representing the problem. The file domain.lp can only contain facts and constant definitions, but no conditional rules or constraints.

Step 3. Encode the planning problem in telingo, but separate the general encoding taxi.lp from the different problem instances dom01.lp, dom02.lp, you try. Each execution would look like

    telingo taxi.lp domain.lp

Notice that each problem instance may have now multiple solutions or valid plans. The plans must be expressed as sequences of sets of following actions move(T,u), move(T,d), move(T,l), move(T,r), pick(T), drop(T), wait(T). For instance, a possible plan printed by telingo for the example above can look like file solution.txt.

Finally, if you have installed the python library pygame, you can also draw a graphical representation using the files drawtaxi.py and picstaxi.zip (to be added) as follows. First, unzip de pictures file, and then call the program using a domain file domXX.txt and an solution file just containing the text output generated by telingo. As an example, try:

    python3 drawtaxi.py domain.txt solution.txt

Step 4. Experiment with additional constraints to reduce the combinations to be tried. For instance, try to write the heuristic rule "never pick the same person twice in the same taxi". Optional: try writing these rules using temporal operators within &tel{...} expressions.

Assessment and Delivery