Thermometers puzzle

This assignment consists in solving the thermometers puzzle (try here an online game) described as follows. We have a grid of n x n cells that is initially filled with empty "thermometers". Each thermometer is an horizontal or vertical line (of size >1) with a "bulb" in one of its ends. The puzzle consists in filling the thermometers with mercury, always starting from their bulb towards their opposite end. Some thermometers can be left partially filled or even empty. The main constraint in the puzzle is that the number of cells filled with mercury in each row and each column must coincide with the respective numbers shown outside the grid.

The following images show an example of initial configuration of a puzzle (4 x 4) and the final solution.

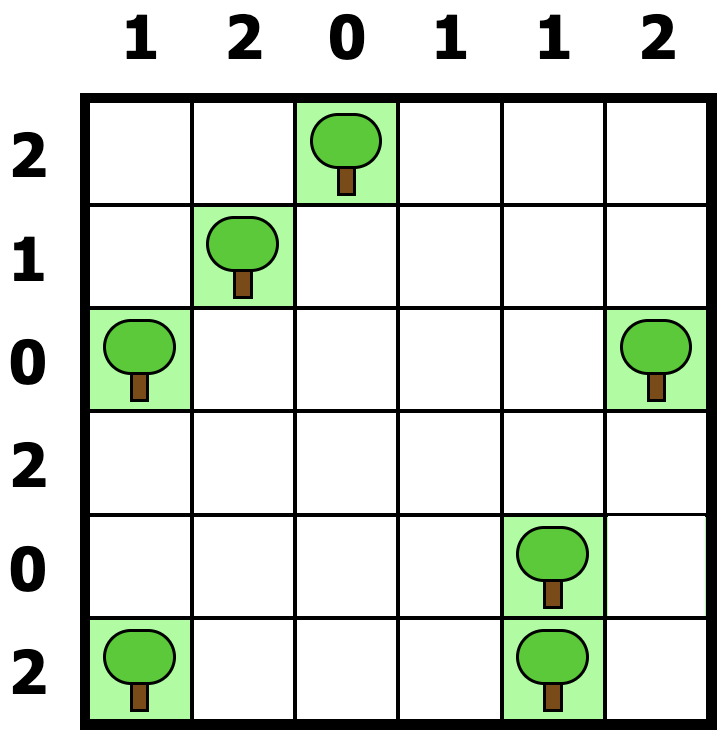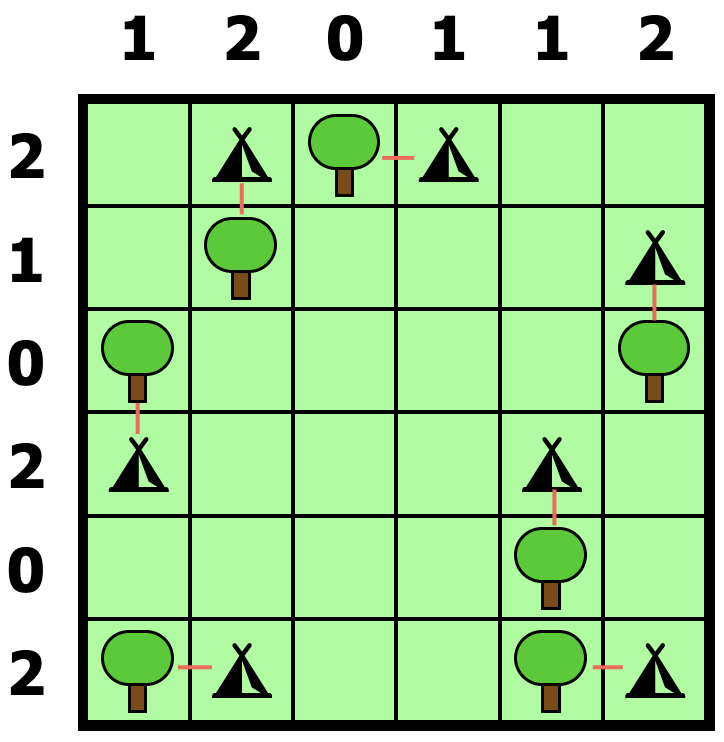Initial configuration	Solved puzzle

Step 1. Each input instance is an ASCII file containing a squared grid (n x n) with the following format. The file contains n lines (the rows) and each line contains n characters (the columns) ended by a newline. Each cell contains a character that can be:

•  U D R L = is a thermometer bulb whose output is oriented up, down, right or left, respectively
• ^ v = are vertical portions of a thermometer respectively pointing up or down
  
• > < = are horizonatl portions of a thermometer respectively pointing right or left

The last two lines contain the numbers associated to columns (first line) and rows (second line) separated by blank spaces.

The following shows the input format for the initial configuration above:

^R>> UR>D DDDv vvvv 3 2 1 1 1 3 2 1

The file examplesthermo.zip contains several input files and their solutions.

Step 2. Write a python program encode.py to transform each input ASCII file into a logic program containing facts. For instance:

python3 encode.py dom01.txt domain.lp

will transform the example above into the set of facts for the predicates you decide to use for representing the problem. The file domain.lp can only contain facts and constant definitions, but no conditional rules or constraints.

Step 3. Encode the tents problem in clingo in a file called thermo.lp. You can use

clingo 0 thermo.lp domain.lp

to obtain all the answer sets. You should check that each puzzle should have a unique solution. You can use the following file decode.py that allows printing the solution as an output text file:

python3 decode.py thermo.lp domain.lp

To use this program, you need output facts like fill(X,Y) to represent that the cell at X, Y is filled with mercury. You also need a predicate dim(N) to specify the size of the grid -- in the example above, dim(4). The result produced by this program will have the form

.x.. xx.x x.x. x...

Where 'x' represents a filled cell.

Finally, if you have installed the python library pygame, you can also draw a graphical representation using the files drawthermo.py and pics.zip (to be added) as follows. First, unzip de pictures file, and then call the program using a domain file domXX.txt and the output from decode.py (or a solXX.txt file instead):

unzip pics.zip python3 drawthermo.py dom01.txt output.txt

Optional (curved thermometers)

As optional work (it may be used to increase the final course grade with 2 pts), you can also consider the variant of the puzle where thermometers are not straight, but may also turn instead. This is an example of this variant:

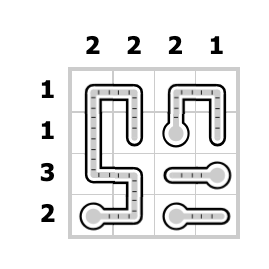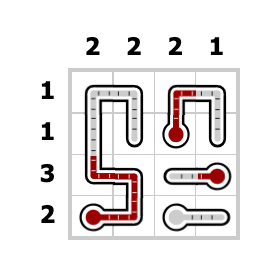Initial configuration	final configuration

For this variant, we will extend the input files as follows:

•  0 1 2 3 = they correspond to the four clockwise rotations of an "L" shape, that is, the respective turns└ ┏  ┐┘

The initial state above would correspond to the input file:

1212 ^vUv 02<L R3R> 2 2 2 1 1 1 3 2

Solutions are represented in the same way as before (you can use the same decode.py program). In this case, the puzzle solution would correspond to:

..x. ..x. xx.x xx..

NEW: examplesthermob.zip contains four new domains (and their solutions) for the curved version of the puzzle.

Assessment & delivery