Se escribe ![]() para una definición inductiva válida
en un contexto
para una definición inductiva válida
en un contexto ![]() ,
un contexto de definiciones
,
un contexto de definiciones ![]() ,
y un contexto de constructores
,
y un contexto de constructores ![]() .
.
Conjunción: ![]()
naturales: ![]()
listas de elementos de A: ![]()
En general, ![]() ,
las reglas de tipado
,
las reglas de tipado
son:
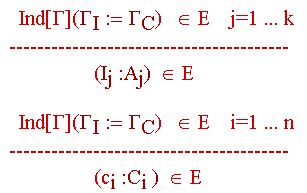
Lo cual significa que si introducimos un tipo inductivo
en nuestro entorno E, quedan también incorporados al mismo el contexto
de definiciones y el de constructores. Pero cada definición inductiva
incorpora también nuevos teoremas que implementan, por ejmplo,
el proceso de inducción.
Coq < Variables
A,B:Prop.
A is assumed
B is assumed
Coq < Inductive
and_AB:Prop := conj_AB:A->B->(and_AB).
and_AB_ind is defined
and_AB_rec is defined
and_AB is defined
Coq < Check and_AB_ind.
and_AB_ind
: (P:Prop)(A->B->P)->and_AB->P
Esto significa, por ejemplo, que si tenemos que probar una proposición como and_AB->P, y tenemos una prueba H: and_AB, entonces basta que encontremos una prueba de (A->B->P)pues (and_AB_ind P)aplicado a dicha prueba nos proporciona una de nuestra proposición.
Este proceso constituirá la esencia de las tácticas de eliminación Elim H. Por ejemplo:
Coq < Lemma foo:and_AB
-> Propiedad.
1 subgoal
============================
and_AB->Propiedad
foo < Intro.
1 subgoal
H : and_AB
============================
Propiedad
foo < Elim H.
1 subgoal
H : and_AB
============================
A->B->Propiedad
foo <
Inductive nat
: Set := O : nat | S : nat->nat.
nat_ind
is defined
nat_rec
is defined
nat_rect
is defined
nat
is defined
Check
nat.
nat
: Set
Check
O.
O
: nat
Check
S.
S
: nat->nat
Check nat_ind.
nat_ind
: (P:nat->Prop)
(P O)->((n:nat)(P n)->(P (S n)))->(n:nat)(P n)
Por ejemplo:
Coq < Variable
predicado:nat -> Prop.
predicado is assumed
Coq < Lemma fooo:(n:nat)(predicado
n).
1 subgoal
============================
(n:nat)(predicado
n)
fooo < Intro.
1 subgoal
n : nat
============================
(predicado
n)
fooo < Elim n.
2 subgoals
n : nat
============================
(predicado
O)
subgoal 2 is:
(n:nat)(predicado
n)->(predicado (S n))
fooo <
Coq
< Variable A:Set.
A
is assumed
Coq
< Inductive List:Set:=nula:List|constr:A->List->List.
List_ind
is defined
List_rec
is defined
List_rect
is defined
List
is defined
Coq < Check nula.
nula
: List
Coq < Check constr.
constr
: A->List->List
Coq < Check List.
List
: Set
Coq < Variable
propiedad_listas:List -> Prop.
propiedad_listas
is assumed
Coq < Lemma
foooo:(l:List)(propiedad_listas l).
1 subgoal
============================
(l:List)(propiedad_listas
l)
foooo < Intro.
1 subgoal
l : List
============================
(propiedad_listas
l)
foooo < Elim l.
2 subgoals
l : List
============================
(propiedad_listas
nula)
subgoal 2 is:
(a:A)(l:List)(propiedad_listas
l)->(propiedad_listas (constr a l))
foooo <
Definiciones inductivas con parámetros: ![]() significa una definición inductiva
válida en un contexto
significa una definición inductiva
válida en un contexto ![]() con parámetros
con parámetros ![]() ,
un contexto de definiciones
,
un contexto de definiciones ![]() y un contexto de constructores
y un contexto de constructores ![]() .
.
![]() está bien formado si y sólo si
está bien formado si y sólo si ![]() lo está.
lo está.
Si ![]() es
es ![]() ,
un objeto en
,
un objeto en ![]() aplicado a
aplicado a
![]() se comportará
como el objeto correspondiente de
se comportará
como el objeto correspondiente de
Ind-Const
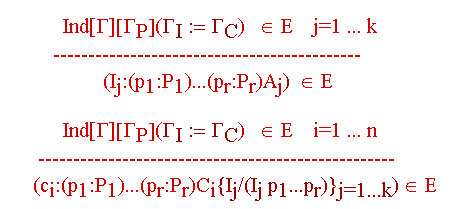
Coq
< Inductive and [A:Prop; B:Prop] : Prop := conj
: A->B->(and A B).
and_ind
is defined
and_rec
is defined
and
is defined
Coq < Print and_ind.
and_ind =
[A,B,P:Prop]
[f:A->B->P][a:(and A B)]Cases a of (conj x x0) => (f x x0) end
: (A,B,P:Prop)(A->B->P)->(and A B)->P
Coq < Print and_rec.
and_rec =
[A,B:Prop]
[P:Set][f:A->B->P][a:(and A B)]Cases a of (conj x x0) => (f x
x0) end
: (A,B:Prop)(P:Set)(A->B->P)->(and A B)->P
Coq
< Variable propiedad:Prop.
propiedad
is assumed
Coq
< Lemma Foo:(A,B:Prop)(A/\B)->propiedad.
1
subgoal
============================
(A,B:Prop)(and A B)->propiedad
Foo
< Intros.
1
subgoal
A : Prop
B : Prop
H : (and A B)
============================
propiedad
Foo
< Elim H.
1
subgoal
A : Prop
B : Prop
H : (and A B)
============================
A->B->propiedad
Foo
<
| DESTRUCTORES: Como se ve en el ejemplo anterior, los tipos inductivos
proveen un teorema (en este caso and_ind)
que nos permite eliminar (destructor) el tipo introducido. La idea es que
si queremos demostrar un cierto objetivo P, y tenemos una prueba H:(A/\B),
entonces Elim H nos da como subgoal (A->B->P), y ello porque aplicando
and_ind A B P:(A->B->P)->(A/\B)->P.
Lo análogo en el campo Set, sería and_rec. CONSTRUCTORES: Si se como objetivo G un tipo de dato construido por "constructores" C1,...,Cn (por ejemplo conj:A->B->(A/\B)), entonces Intros;Apply Ci equivale a Constructor ci. Suele tener nombres especiales. Por ejemplo, Apply conj = Split, Apply introl = Left o Apply intror=Right. En general la táctica Constructor i |
Praeclarum
< Intros x y z t h; Elim h; Intros H' H'0; Clear h.
1
subgoal
x : Prop
y : Prop
z : Prop
t : Prop
H' : x->z
H'0 : y->t
============================
(and x y)->(and z t)
Praeclarum
< Intro h; Elim h; Intros H'1 H'2; Clear h.
1
subgoal
x : Prop
y : Prop
z : Prop
t : Prop
H' : x->z
H'0 : y->t
H'1 : x
H'2 : y
============================
(and z t)
Praeclarum
< Split.
2
subgoals
x : Prop
y : Prop
z : Prop
t : Prop
H' : x->z
H'0 : y->t
H'1 : x
H'2 : y
============================
z
subgoal
2 is:
t
Praeclarum < Show 2.
subgoal 2 is:
x : Prop
y : Prop
z : Prop
t : Prop
H' :
x->z
H'0 :
y->t
H'1 :
x
H'2 :
y
============================
t
Praeclarum
< Apply H';Assumption.
1
subgoal
x : Prop
y : Prop
z : Prop
t : Prop
H' : x->z
H'0 : y->t
H'1 : x
H'2 : y
============================
t
Praeclarum
< Apply H'0;Assumption.
Subtree
proved!
Praeclarum
< Qed.
(Intros
x y z t h; Elim h; Intros H' H'0; Clear h).
(Intro
h; Elim h; Intros H'1 H'2; Clear h).
Split.
(Apply
H'; Assumption).
(Apply H'0; Assumption).
Praeclarum
is defined
Coq
< Print Praeclarum.
Praeclarum =
[x,y,z,t:Prop]
[h:(and
x->z y->t)]
(and_ind
x->z y->t (and x y)->(and z t)
[H':x->z]
[H'0:y->t]
[h0:(and x y)]
(and_ind x y (and z t)
[H'1:x][H'2:y](conj z t (H' H'1) (H'0
H'2)) h0) h)
: (x,y,z,t:Prop)(and x->z y->t)->(and x y)->(and
z t)
Inductive
List [A:Set]:Set :=
Nil:(List
A)|Cons:A->(List A)->(List A).
List_ind
is defined
List_rec
is defined
List_rect
is defined
List
is defined
Check Nil.
Nil
: (A:Set)(List A)
Check Cons.
Cons
: (A:Set)A->(List A)->(List A)
Check List.
List
: Set->Set
Coq < Inductive
Long [A:Set]: (List A)->nat->Prop :=
Lnil:(Long A (Nil A) O)
| Lcons : (a:A)(l:(List A)) (n:nat) (Long A l n)->(Long A (Cons A a l)
(S n)).
Long_ind is defined
Long is defined
Coq < Check Long.
Long
: (A:Set)(List A)->nat->Prop
Coq < Check Lnil.
Lnil
: (A:Set)(Long A (Nil A) O)
Coq < Check Lcons.
Lcons
: (A:Set)
(a:A)
(l:(List A))(n:nat)(Long A l n)->(Long A (Cons A a l) (S n))
La definición del cuantificador universal es un ejemplo de definición. No es un tipo inductivo.
Coq < Definition
all := [A:Set][P:A->Prop](x:A)(P x).
all is defined
El cuantificador Existencial sí es inductivo.
Coq < Inductive
ex [A:Set;P:A->Prop] : Prop := ex_intro : (x:A)(P x)->(ex A P).
ex_ind is defined
ex is defined
Coq < Check ex_ind.
ex_ind
: (A:Set)(P:A->Prop)(P0:Prop)((x:A)(P x)->P0)->(ex A P)->P0
Coq < Inductive
ex2 [A:Set;P,Q:A->Prop] : Prop := ex_intro2 : (x:A)(P x)->(Q x)->(ex2 A
P Q).
ex2_ind is defined
ex2 is defined
Coq < Check ex2_ind.
ex2_ind
: (A:Set)
(P,Q:A->Prop)(P0:Prop)((x:A)(P x)->
(Q x)->P0)->(ex2 A P Q)->P0
Se permiten las siguientes abreviaturas:
| (ALL x:A | P) | (all A [x:A]P) |
| (ALL x | P) | (all A [x:A]P) |
| (EX x:A | P) | (ex A [x:A]P) |
| (EX x | P) | (ex A [x:A]P) |
| (EX x:A | P & Q) | (ex2 A [x:A]P [x:A]Q) |
| (EX x | P & Q) | (ex2 A [x:A]P [x:A]Q) |
Hay cuantificador Existencial en el dominio Set
Inductive sig [A:Set; P:A->Prop] :
Set :=
exist
: (x:A)(P x)->(sig A P)
que se escribe {x:A | (P x)}