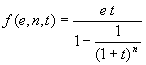
Esta proliferación cuesta cara a la industria del Software: hace difícil la concepción de sistemas integrando módulos ya desarrollados en lenguajes diferentes, demanda la creación de interfaces, pasarelas y otros traductores y hace del mantenimiento de estos sistemas híbridos un verdadero rompecabezas. Para poner fín a esta discordancia, el ministerio de defensa de los EEUU puso en marcha, en 1978, un concurso con el fín de elegir un lenguaje de programación único para imponerlo como lenguaje de desarrollo para todo su software. Con esta idea de un "esperanto" de la programación, el ministerio de defensa americano se reencontraba con el sueño secular de una lengua artificial, perfecta y universal. Lengua que el teólogo Raymundo Lulio había ya intentado construir en el siglo trece. Este concurso (retomado al año siguiente por un equipo dirigido por Jean Ichbiah) permitió la creación del lenguaje Ada, el cual es todavía bastante popular, pero que ha fracasado en su vocación de universalidad.
No obstante, limitado al dominio restringido de la programación,
este sueño de un lenguaje universal no debería considerarse
utópico. La gran mayoría de los músicos utilizan el
mismo lenguaje para escribir sus partituras. Análogamente, los matemáticos
de todos los paises utilizan un lenguaje común, lo que no le impide
a este lenguaje el evolucionar en función de las necesidades, ni
que cada uno lo utilice con un estilo propio. Si en el dominio de la programación
no hemos alcanzado aún esa unidad, ello puede ser una señal
de que no hemos comprendido bien aún qué es un programa o
un lenguaje de programación.
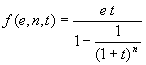
donde f(e,n,t) es el importe de las mensualidades, e la cantidad prestada, n el número de mensualidades y t la tasa de interés mensual.
Un programa es pues cualquier cosa que permite asociar
una magnitud (el valor de salida) a una o varias magnitudes (los valores
de entrada). Un tal objeto que permite asociar una magnitud a otras magnitudes
es lo que los matemáticos denominan una función. El
programa que utiliza el banco no es otra cosa que la función f
que
asocia el número 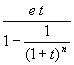 a los números e, n y t. Desde este punto de vista,
un lenguaje de programación no es otra cosa que un lenguaje de definición
de funciones.
a los números e, n y t. Desde este punto de vista,
un lenguaje de programación no es otra cosa que un lenguaje de definición
de funciones.
La necesidad misma de concebir lenguajes de
programación se encuentra entonces puesta en cuestión: si
no se trata más que de definir funciones ¿para qué
crear un nuevo lenguaje, dado que el lenguaje matemático ordinario
lleva haciendo esto tan bien desde hece varios siglos?
![]()
Esta es la forma cómo los matemáticos definen la función
que a un número le asocia su cuadrado: el término x´x
indica
el valor asociado por la función al valor x.
El valor que
toma f en 3, por ejemplo, se obtiene reemplazando el argumento formal
x por el argumento real 3 en ese término, lo cual da 3 ´
3.
Esta notación
existe casi literalmente en la mayor parte de los lenguajes de programación.
Por ejemplo, en el lenguaje Pascal, concebido en 1970 por Niklaus Wirth
y su equipo, se define esta misma función por el texto:
function f (x:integer) : integer;
begin
f:= x*x
end;
Pero, las funciones que se pueden definir explícitamente
forman una pequeña parte de las funciones que se necesitan en matemáticas
o informática. Por ejemplo, la función potencia que
asocia el número ![]() a
los números x y n no se puede definir explícitamente.
En la escuela hemos aprendido que esta función tiene la curiosa
definición:
a
los números x y n no se puede definir explícitamente.
En la escuela hemos aprendido que esta función tiene la curiosa
definición:
![]()
Estos mismos puntos suspensivos han sido utilizados más tarde, cuando hemos aprendido ls definición de la función Seno que era:
![]()
Los puntos suspensivos que se utilizan en estas dos definiciones no tienen en absoluto el mismo significado: en la de la definición del Seno expresan una definición como límite de una serie mientras que en la de la función potencia expresan una definición recursiva:
potencia(x,0)=1
potencia(x,n+1)=x´ potencia(x,n)
Dicho de otra forma, la función potencia se define como
la única función verificando estas dos ecuaciones.
|
Sin embargo, no es suficiente dar un sistema de ecuaciones para definir una función. Así la ecuación
f(x)=f(x)
no es una definición correcta pues esta ecuación la verifican muchas funciones. Analogamente la ecuación
f(x)=1+f(x)
no es tampoco una definición correcta pues no la verifica
ninguna función. La definición de la función potencia
no
será pues correcta hasta que se demuestre que existe una función
única que verifique sus ecuaciones.
Se comprende mejor entonces el mecanismo verdaderamente
utilizado para definir funciones en matemáticas. Se comienza par
dar un sistema de ecuaciones, o más generalmente una propiedad,
que debe verificar la función, se muestra a continuación
que existe una única función que verifica esa propiedad,
y se da finalmente un nombre a la función.
Para atribuir un nombre a la función se utiliza
en general una frase de la forma "se llamará potencia a la
única función que verifica las siguientes propiedades ..."
Salvo su nombre, no hay ninguna expresión para designar la función
en cuestión. Desde un punto de vista más formal (que es el
propio de los que tratan de concebir lenguajes de programación)
se puede denotar [f | P(f)] el único objeto que verifica
la propiedad P de la misma manera que se denota {f | P(f)}
el conjunto de los objetos que verifican esta propiedad. Esta notación
que permite expresar un objeto por medio de una descripción se llama
operador
de descripciones.
La función potencia se definiría pues
como:
![]()
Del mismo modo que la gramática del lenguaje
matemático prohibe formar la expresión 1/0 que no tiene sentido,
prohibe también la utilización del operador de descripciones
con una propiedad que no es verificada por ningún objeto. Es, por
ejemplo, imposible formar la expresión ![]() .
(De hecho, no es esencial que estas expresiones carentes de sentido sean
prohibidas por la gramática. Se puede adoptar también la
convención según la cual la expresión 1/0 es correcta
y designa un objeto matemático cualquiera: el conjunto vacío,
el número 0, ... lo que importa es que la propiedad x´1/x
= 1 sea verdadera únicamente cuando x sea diferente de
0).
.
(De hecho, no es esencial que estas expresiones carentes de sentido sean
prohibidas por la gramática. Se puede adoptar también la
convención según la cual la expresión 1/0 es correcta
y designa un objeto matemático cualquiera: el conjunto vacío,
el número 0, ... lo que importa es que la propiedad x´1/x
= 1 sea verdadera únicamente cuando x sea diferente de
0).
Cuando varios objetos verifican la propiedad utilizada,
se pueden adoptar distintas convenciones. La utilización del operador
de descripciones está, en general, prohibida en este caso, pero
una regla más liberal autoriza esta utilización y permite,
por ejemplo, la formación de la expresión [x | x´x
= 9] que ya no se lee "el número x tal que x´x
= 9" sino "un número x tal que x ´x
= 9". El operador de descripciones se llama entonces operador de
elección, operador e de
Hilbert o operador t
de
Bourbaki. El número [x | x ´x
= 9] vale 3 ó -3, sin que se sepa si vale 3 ó -3. Así,
no se puede demostrar [x | x ´x
= 9]=3 ni [x | x´x = 9]=-3
pero se puede demostrar [x | x´x
= 9] ![]() {3,-3}.
{3,-3}.
Cuando un cliente demanda un programa a un informático, le
debe explicar lo que debe hacer ese programa. Esta explicación
se llama el cuaderno de carga o también la especificación
del programa. Por ejemplo, cuando un industrial pide a una sociedad de
servicios un programa de inversión de matrices, la especificación
cabe en una línea
La ejecución de los programas
Cuando se ha terminado un programa, es preciso poder ejecutarlo. Así, si se prestan 30 000 Francos a 24 meses a un interés mensual de 0.64% ( lo que corresponde a una tasa anual del 8%), el programa mencionado antes debe indicar que las mensualidades serán de 1353 Francos. En efecto
Los lenguajes de programación tradicionales no proponen pues
directamente operador de descripciones, sinó que proponen construcciones
más restringidas que corresponden a casos particulares de utilización
de este operador.
Casi todos los lenguajes de programación
permiten definir funciones por recurrencia con la ayuda de bucles. Así,
en Pascal, se puede definir la función potencia por el bucle:
r:= 1; for i:=1 to n do r:=x*r
la ejecución de un tal programa demanda repetir n veces
la operación que se encuentra en el bucle, es decir el calcular
sucesivamente ![]() .
.
Otros lenguajes, como el lenguaje Lisp (concebido
en 1962 por John Mc Carthy y su equipo) o su sucesor el lenguaje ML (sugerido
en 1966 por Peter Landin y concebido en 1978 por Robin Milner y su equipo)
proponen la utilización de definiciones recursivas, es decir, simular
la utilización de la función a definir en su propia definición.
Por ejemplo, en ML, se define la función potencia así:
let rec potencia = fun x n -> if n=0 then 1 else x*(potencia x (n-1));;
Como es incorrecto definir un objeto utilizando el mismo objeto a definir, un tal programa debe entenderse como una definición implícita utilizando el operador de descripciones:
![]()
Definir así las funciones recursivamente significa utilizar el
operador de descripciones en el caso particular donde las propiedades son
de la forma f = G(f). Ejecutar un tal programa exige ejecutar el
cuerpo de la definición G(f) llamando a la función
misma cuando se utiliza en la propia definición.
Contrariamente a los bucles, este mecanismo permite
salir de los límites de utilización del operador de descripciones
autorizado por la gramática del lenguaje matemático (lo cual
impone que existe un único objeto verificando la propiedad). Así
los programas en ML:
let rec f = fun x -> f x;;
let rec f = fun x -> 1 + (f x);;
corresponden a las definiciones "ilegales" ![]() y
y ![]() . Esto
se traduce en el hecho de que la ejecución de estos programas lleva
a cálculos infinitos (calcular f(0) demanda calcular antes
f(0)
lo
cual exige calcular antes ....). Para dar un sentido a estas definiciones
recursivas incorrectas, Dana Scott propuso en 1970 añadir al espacio
de valores, un valor suplementario "indefinido" y ver las definiciones
recursivas como funciones sobre este espacio de valores extendido, las
dos definiciones anteriores se convierten en "legales" y corresponden a
la misma función constantemente igual a ese valor "indefinido",
Dicho de otro modo, la ejecución de estos dos programas sobre cualquier
entrada lleva siempre a cálculos infinitos.
. Esto
se traduce en el hecho de que la ejecución de estos programas lleva
a cálculos infinitos (calcular f(0) demanda calcular antes
f(0)
lo
cual exige calcular antes ....). Para dar un sentido a estas definiciones
recursivas incorrectas, Dana Scott propuso en 1970 añadir al espacio
de valores, un valor suplementario "indefinido" y ver las definiciones
recursivas como funciones sobre este espacio de valores extendido, las
dos definiciones anteriores se convierten en "legales" y corresponden a
la misma función constantemente igual a ese valor "indefinido",
Dicho de otro modo, la ejecución de estos dos programas sobre cualquier
entrada lleva siempre a cálculos infinitos.
A diferencia del lenguaje ML que utiliza el operador
de descripciones para definir la función misma, el lenguaje Prolog
(concebido en 1973 por Alain Colmerauer y su equipo) utiliza el operador
de descripciones únicamente para definir el valor tomado por la
función, es decir, el valor de salida del programa. Por ejemplo
la función
potencia no será ya definida por un término
de la forma [f | P(f)] donde P es una propiedad característica
de esta función, sino por un término de la forma
siguiente :
![]()
que recuerda al programa en prolog
e(A,0,1).
e(A,P,S) :- Q is P-1, e(A,Q,R),
S is A*R.
Le ejecución del programa demanda resolver la ecuación
Q(x,n,y)
en y. Esta ecuación al tratar sobre un valor y no sobre una
función, se puede resolver de una forma bastante sistemática.
Más generalmente los lenguajes de programación
con restricciones introducidos por Joxan Jaflar y Jean-Louis Lassez en
1987 son extensiones del Prolog que utilizan algoritmos especiales para
la resolución de estas ecuaciones.
Se pueden ver pues los lenguajes de programación tradicionales
como restricciones del lenguaje matemático. El operador de descripciones
no se utiliza más que en ciertos casos particulares, la restricción
escogida distingue unos lenguajes de otros. La ventaja de esta restricción
es que permite ejecutar los programas. Su inconveniente es que limita la
expresividad de los programadores. Un lenguaje de programación es
siempre un compromiso entre la potencia de la expresión y la posibilidad
de ejecución.
La cuestión que se puede entonces proponer
es la de saber si es posible encontrar reglas de cálculo para la
totalidad del lenguaje matemático, es decir, para el operador de
descripciones en toda su generalidad. La respuesta negativa a esta pregunta
la da la teoría de la calculabilidad: un resultado debido a Alan
Turing e independientemente a Alonzo Church y Stephen Kleene, en 1936,
demuestra, en efecto, que existen funciones que no son calculables. El
ejemplo más célebre de función no calculable es el
problema de la parada: el imposible construir un programa que tome como
entrada otro programa e indique si lleva a cálculos finitos o infinitos.
Se puede pues definir la función
h = [f | para todo p, si p termina entonces f(p)=0 y sinó f(p)=1]
pero no hay regla de cálculo que nos dé sistemáticamente
el valor de h(p).
Para que esta definición sea correcta,
es preciso demostrar que una única función verifica la especificación.
Esta demostración utiliza el hecho de que para todo programa p,
o
bien p termina o bien p no termina. Este hecho es, él
mismo, establecido por una regla de razonamiento, el tercio excluso, que
indica que para toda proposición P se puede demostrar "P
o no P" sin saber demostrar "P" ni "no P".
|
Al comienzo del siglo veinte, una escuela de matemáticos,
llamados intuicionistas o constructivistas, han criticado
vívamente esta regla de razonamiento. ¿Cómo puede
pretenderse saber que la proposición "P o no P" es cierta,
si no se sabe ni que "P" es cierta, ni que "no P" es cierta?
Del mismo modo, ¿cómo se puede pretender haber definido el
número h(p) si no se sabe si este número vale 0 ó
1? Para los intuicionistas la definición de la función h
de antes es simplemente incorrecta. Detrás de Luitzen Egbertus
Jan Brouwer, el jefe de filas de la escuela intuicionista, forman matemáticos
importantes como Hermann Weyl o Andreï Kolmogorov.
Un teorema de Setphen Kleene demuestra que, cuando
se abandona el tercio excluso, todas las funciones que se pueden definir
con el operador de descripciones son calculables. Este teorema toma naturalmente
formas diferentes en función de la teoría en la que se coloca
para demostrar la existencia y la unicidad de la función descrita.
Dicho de otro modo, el tercio excluso es indispensable para demostrar la
existencia de una función no calculable. Cuando se abandona el tercio
excluso, entonces es posible encontrar reglas de cálculo para el
operador de descripciones en toda su generalidad. Cuando se define una
función [f | P(f) ] después de haber dado una
demostración constructiva p de la existencia de una función
verificando la propiedad P, se puede ejecutar ese programa. Para
ello se aplica a la demostración p y al valor de entrada,
una transformación llamada eliminación de cortaduras.
El primer procedimiento de eliminación de cortaduras ha sido propuesto
en 1934 por Gerard Gentzen para las demostraciones expresadas en la aritmética.
Después, se ha generalizado a muchas otras teorías. En particular,
Jean-Yves Girard propuso en 1971 un procedimiento de eliminación
de cortaduras para la aritmética de orden superior, que es una variante
de la teoría de conjuntos.
Aparece entonces una nueva metodología de
la programación: se comienza por especificar la función a
programar por una propiedad P, se da a continuación una demostración
constructiva p de la existencia de una función que verifica
esta propiedad y se define a continuación el programa [f
| P(f)]. La ejecución de este programa consiste en eliminar
las cortaduras en la demostración p. Esta aproximación
es la base del lenguaje AF2 sugerido por Daniel Leivant y concebido por
Michel Parigot en 1987.
whisky, gin, vodka
gin, whisky, vodka
gin, vodka, whisky
es un programa mal concebido. Todos los programadores saben que la primera
lista es inútil una vez que se construye la segunda y que por lo
tanto se puede ordenar "en su propio espacio" es decir utilizando la misma
zona de memoria para guardar los estados sucesivos de la lista.
Si nos contentamos con demostrar la existencia de
una función que asocia una permutación ordenada a cada lista
¿cómo saber si la ejecución de este programa ordenará
las listas "en su propio espacio" o recopiará la lista en cada etapa?
Las matemáticas no son un lenguaje de programación muy consciente
de la gestión de los recursos.
La programación en lenguaje matemático
propone nuevos desafíos a las teorías de la compilación,
del análisis estático y de la transformación de programas
¿Cómo transformar un programa desarrollado en lenguaje matemático
en un programa equivalente en lenguaje máquina pero que gestione
eficazmente sus recursos y no efectúe cálculos inútiles?
Un útil esencial para resolver estas cuestiones
es sin duda la lógica lineal, desarrollada por Jean-Yves Girard
en 1987. Según esta teoría , las matemáticas no son
muy conscientes de la gestión de los recursos porque "las hipótesis
no se gastan cuando se utilizan". Así en las lógicas tradicionales
las proposiciones "P" y "P & P" son equivalentes. En
lógica lineal estas dos proposiciones no son ya equivalentes, suponer
la primera permite utilizar una única vez la hipótesis P
en una demostración mientras que suponer la segunda permite utilizar
dos veces esta hipótesis. En la demostración de la existencia
de una función de ordenación, una hipótesis utilizada
una única vez revela que una vez que se ha utilizado la lista, puede
destruirse, lo cual es exactamente la información necesaria para
programar la ordenación "en place". La lógica lineal ya ha
sido utilizada para gestionar los recursos en compiladores para el lenguaje
ML. Este tipo de análisis debe ser extendido al caso de la programación
en lenguaje matemático.
Parece que la vuelta hacia un punto de vista más operacional no significa un verdadero problema. Que 12+23 se calcule a 35 como hecho diferenciado de que sea igual a 35 es una idea largamente compartida. La toma en cuenta de las demostraciones como objetos matemáticos no parece proponer un verdadero problema. En el transcurso de la historia, los matemáticos han integrado siempre los objetos extramatemáticos que utilizaban. Las funciones que eran utilizadas desde la antigüedad para designar las magnitudes (por ejemplo en la expresión "Seno(0)") se convirtieron en objetos matemáticos de pleno derecho con Newton y Leibniz, y también con Euler, cuando se hizo posible expresar propiedades de las propias funciones (y decir que la función Seno es, por ejemplo, continua, periódica, derivable, etc.). Además, parece que tener las demostraciones como objetos de pleno derecho resuelve problemas fuera del campo de la programación, y en particular que ciertas formas del axioma de la elección aparezcan como teoremas.
- la vuelta a un punto de vista más operacional y la toma en consideración de la noción de cálculo,
- el abandono del "tercio excluso" y la restricción a las matemáticas constructivas,
- la toma en cuenta de las demostraciones como objetos matemáticos de pleno derecho.