Definiciones Inductivas y sus reglas de eliminación-contrucción.

Definiciones inductivas sin parámetros:

Se escribe para una definición inductiva válida en un contexto , un contexto de definiciones , y un contexto de constructores.

Conjunción: 
naturales: 

listas de elementos de A: 

En general, , las reglas de tipado
son:


 


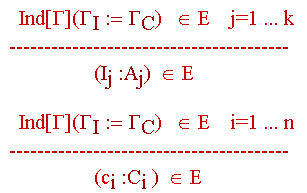
Lo cual significa que si introducimos un tipo inductivo en nuestro entorno E, quedan también incorporados al mismo el contexto de definiciones y el de constructores.
Coq < Variables A,B:Prop.
A is assumed
B is assumed
Coq < Inductive and_AB:Prop := conj_AB:A->B->(and_AB).
and_AB_ind is defined
and_AB_rec is defined
and_AB is defined
Coq < Check and_AB.
and_AB
     : Prop
Coq < Check conj_AB.
conj_AB
     : A->B->and_AB

Pero cada definición inductiva incorpora también  nuevos teoremas que implementan, por ejemplo, el proceso de prueba por inducción.

and_AB_ind is defined
and_AB_rec is defined
and_AB is defined

Coq < Check and_AB_ind.
and_AB_ind
     : (P:Prop)(A->B->P)->and_AB->P

Esto significa, por ejemplo,  que si tenemos que probar una proposición como  and_AB->P, y tenemos una prueba H:and_AB, entonces basta que encontremos una prueba de  (A->B->P)pues (and_AB_ind P)aplicado a dicha prueba nos proporciona una de nuestra proposición.

Este proceso constituirá la esencia de las tácticas de eliminación Elim H. Por ejemplo:

Coq < Lemma foo:and_AB -> Propiedad.
1 subgoal

  ============================
   and_AB->Propiedad

foo < Intro.
1 subgoal

  H : and_AB
  ============================
   Propiedad

foo < Elim H.
1 subgoal

  H : and_AB
  ============================
   A->B->Propiedad

foo <
 
 
 
 
 

Inductive nat : Set := O : nat | S : nat->nat.
nat_ind is defined
nat_rec is defined
nat_rect is defined
nat is defined
Check nat.
nat
     : Set
Check O.
O
     : nat
Check S.
S
     : nat->nat

Check nat_ind.
nat_ind
     : (P:nat->Prop)
        (P O)->((n:nat)(P n)->(P (S n)))->(n:nat)(P n)

Por ejemplo:

Coq < Variable predicado:nat -> Prop.
predicado is assumed
Coq < Lemma fooo:(n:nat)(predicado n).
1 subgoal

  ============================
   (n:nat)(predicado n)

fooo < Intro.
1 subgoal

  n : nat
  ============================
   (predicado n)

fooo < Elim n.
2 subgoals

  n : nat
  ============================
   (predicado O)

subgoal 2 is:
 (n:nat)(predicado n)->(predicado (S n))

fooo <
 
 
 

Coq < Variable A:Set.
A is assumed

Coq < Inductive List:Set:=nula:List|constr:A->List->List.
List_ind is defined
List_rec is defined
List_rect is defined
List is defined
Coq < Check nula.
nula
     : List

Coq < Check constr.
constr
     : A->List->List

Coq < Check List.
List
     : Set

Coq < Variable propiedad_listas:List -> Prop.
propiedad_listas is assumed

 Coq < Lemma foooo:(l:List)(propiedad_listas l).
1 subgoal

  ============================
   (l:List)(propiedad_listas l)

foooo < Intro.
1 subgoal

  l : List
  ============================
   (propiedad_listas l)

foooo < Elim l.
2 subgoals

  l : List
  ============================
   (propiedad_listas nula)

subgoal 2 is:
 (a:A)(l:List)(propiedad_listas l)->(propiedad_listas (constr a l))

foooo <
 

Definiciones inductivas con parámetros:significa una definición inductiva válida en un contexto  con parámetros , un contexto de definiciones  y un contexto de constructores .
está bien formado si y sólo silo está.

Si es, un objeto en  aplicado a
se comportará como el objeto correspondiente de

 Ind-Const

 
Por ejemplo:

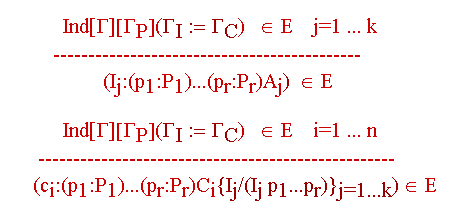
Coq < Inductive and [A:Prop; B:Prop] : Prop := conj : A->B->(and A B).
and_ind is defined
and_rec is defined
and is defined
Coq < Print and_ind.
and_ind =
[A,B,P:Prop]
 [f:A->B->P][a:(and A B)]Cases a of (conj x x0) => (f x x0) end
     : (A,B,P:Prop)(A->B->P)->(and A B)->P

Coq < Print and_rec.
and_rec =
[A,B:Prop]
 [P:Set][f:A->B->P][a:(and A B)]Cases a of (conj x x0) => (f x x0) end
     : (A,B:Prop)(P:Set)(A->B->P)->(and A B)->P

Coq < Variable propiedad:Prop.
propiedad is assumed
Coq < Lemma Foo:(A,B:Prop)(A/\B)->propiedad.
1 subgoal

  ============================
   (A,B:Prop)(and A B)->propiedad

Foo < Intros.
1 subgoal

  A : Prop
  B : Prop
  H : (and A B)
  ============================
   propiedad

Foo < Elim H.
1 subgoal

  A : Prop
  B : Prop
  H : (and A B)
  ============================
   A->B->propiedad

Foo <
 
 
 
 

DESTRUCTORES: Como se ve en el ejemplo anterior, los tipos inductivos proveen un teorema (en este caso and_ind) que nos permite eliminar (destructor) el tipo introducido. La idea es que si queremos demostrar un cierto objetivo P, y tenemos una prueba H:(A/\B), entonces Elim H nos da como subgoal (A->B->P), y ello porque aplicando and_ind A B P:(A->B->P)->(A/\B)->P.

Lo análogo en el campo Set, sería and_rec.

CONSTRUCTORES: Si se como objetivo G  un tipo de dato construido por "constructores"  C1,...,Cn (por ejemplo conj:A->B->(A/\B)), entonces Intros;Apply Ci equivale a Constructor ci. Suele tener nombres especiales. Por ejemplo, Apply conj = Split, Apply introl = Left o Apply intror=Right. En general la táctica Constructor i 

Se puede definir un tipo sin parámetros haciendo declaraciones locales dentro de una section. Cuando ésta se cierra se produce un proceso de generalización que produce los mismos tipos en el entorno que si hubieramos definido el tipo con parámetros.
 

Por ejemplo:


Coq < Section ejemplo.

Coq < Variables A,B:Prop.
A is assumed
B is assumed

Coq < Inductive and:Prop:=
Coq < conj:A->B->and.
and_ind is defined
and_rec is defined
and is defined

Coq < End ejemplo.
[Cooking #and_ind.cci]
[Cooking #and_rec.cci]
[Cooking #and_rec.fw]
Type and
  : Prop->Prop->Prop
Constant and_ind : (A,B,P:Prop)(A->B->P)->(and A B)->P
Constant and_rec : (A,B:Prop)(P:Set)(A->B->P)->(and A B)->P
Coq < Check and.
and
     : Prop->Prop->Prop

Coq < Check conj.
conj
     : (A,B:Prop)A->B->(and A B)

Otro ejemplo:

Coq < Theorem Praeclarum: (x,y,z,t: Prop) (x -> z) /\ (y -> t) -> x /\ y -> z /\ t.

Praeclarum < Intros x y z t h; Elim h; Intros H' H'0; Clear h.
1 subgoal

  x : Prop
  y : Prop
  z : Prop
  t : Prop
  H' : x->z
  H'0 : y->t
  ============================
   (and x y)->(and z t)

Praeclarum < Intro h; Elim h; Intros H'1 H'2; Clear h.
1 subgoal

  x : Prop
  y : Prop
  z : Prop
  t : Prop
  H' : x->z
  H'0 : y->t
  H'1 : x
  H'2 : y
  ============================
   (and z t)

Praeclarum < Split.
2 subgoals

  x : Prop
  y : Prop
  z : Prop
  t : Prop
  H' : x->z
  H'0 : y->t
  H'1 : x
  H'2 : y
  ============================
   z

subgoal 2 is:
 t

  Praeclarum < Show 2.
subgoal 2 is:

  x : Prop
  y : Prop
  z : Prop
  t : Prop
  H' : x->z
  H'0 : y->t
  H'1 : x
  H'2 : y
  ============================
   t
Praeclarum < Apply H';Assumption.
1 subgoal

  x : Prop
  y : Prop
  z : Prop
  t : Prop
  H' : x->z
  H'0 : y->t
  H'1 : x
  H'2 : y
  ============================
   t

Praeclarum < Apply H'0;Assumption.
Subtree proved!

Praeclarum < Qed.
(Intros x y z t h; Elim h; Intros H' H'0; Clear h).
(Intro h; Elim h; Intros H'1 H'2; Clear h).
Split.
(Apply H'; Assumption).

(Apply H'0; Assumption).

Praeclarum is defined
Coq < Print Praeclarum.
Praeclarum =
[x,y,z,t:Prop]
 [h:(and x->z y->t)]
  (and_ind x->z y->t (and x y)->(and z t)
    [H':x->z]
     [H'0:y->t]
      [h0:(and x y)]
       (and_ind x y (and z t)
         [H'1:x][H'2:y](conj z t (H' H'1) (H'0 H'2)) h0) h)
    : (x,y,z,t:Prop)(and x->z y->t)->(and x y)->(and z t)
 
 
 
 
 
 

Inductive List [A:Set]:Set :=
Nil:(List A)|Cons:A->(List A)->(List A).
List_ind is defined
List_rec is defined
List_rect is defined
List is defined
Check Nil.
Nil
     : (A:Set)(List A)

Check Cons.
Cons
     : (A:Set)A->(List A)->(List A)

Check List.
List
     : Set->Set

Coq < Inductive Long [A:Set]: (List A)->nat->Prop :=
          Lnil:(Long A (Nil A) O)
         | Lcons : (a:A)(l:(List A)) (n:nat) (Long A l n)->(Long A (Cons A a l) (S n)).
Long_ind is defined
Long is defined

Coq < Check Long.
Long
     : (A:Set)(List A)->nat->Prop

Coq < Check Lnil.
Lnil
     : (A:Set)(Long A (Nil A) O)

Coq < Check Lcons.
Lcons
     : (A:Set)
        (a:A)
         (l:(List A))(n:nat)(Long A l n)->(Long A (Cons A a l) (S n))
 
 

La definición del cuantificador universal es un ejemplo de definición. No es un tipo inductivo.

Coq < Definition all := [A:Set][P:A->Prop](x:A)(P x).
all is defined

El cuantificador Existencial sí es inductivo.

Coq < Inductive ex [A:Set;P:A->Prop] : Prop  := ex_intro : (x:A)(P x)->(ex A P).
ex_ind is defined
ex is defined
Coq < Check ex_ind.
ex_ind
     : (A:Set)(P:A->Prop)(P0:Prop)((x:A)(P x)->P0)->(ex A P)->P0
 

Coq < Inductive ex2 [A:Set;P,Q:A->Prop] : Prop := ex_intro2 : (x:A)(P x)->(Q x)->(ex2 A P Q).
ex2_ind is defined
ex2 is defined
Coq < Check ex2_ind.
ex2_ind
     : (A:Set)
        (P,Q:A->Prop)(P0:Prop)((x:A)(P x)->
           (Q x)->P0)->(ex2 A P Q)->P0

Se permiten las siguientes abreviaturas:
 
(ALL x:A | P) (all A [x:A]P)
(ALL x | P) (all A [x:A]P)
(EX x:A | P) (ex A [x:A]P)
(EX x | P) (ex A [x:A]P)
(EX x:A | P & Q) (ex2 A [x:A]P [x:A]Q)
(EX x | P & Q) (ex2 A [x:A]P [x:A]Q)

  Hay  cuantificador Existencial en el dominio Set

Inductive sig [A:Set; P:A->Prop] : Set :=
      exist : (x:A)(P x)->(sig A P)
que se escribe {x:A | (P x)}