Combinación de evidencia: independencia condicional y actualización bayesiana

• supongamos que tenemos
  
  podemos leer o calcularlo con la regla de Bayes
  
  necesitamos conocer . Un diagnóstico puede tratar con muchos variables. Necesitaríamos valores para pares de variables. Este crecimiento exponencial es lo que ha llevado a la necesidad de métodos aproximados de combinación de evidencia
• actualización bayesiana, se incorpora la evidencia paso a paso
  • comenzando por T
    
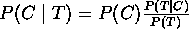
  • al observar A, aplicamos la regla de Bayes usando T como la constante de condicionamento
    
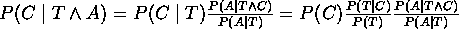
  • cada vez que se observa una nueva evidencia, el grado de creencia en la variable desconocida se multiplica por un factor (la segunda fracción) que depende de la nueva evidencia
  • el problema es que el nuevo factor depende todavía de la evidencia observada anteriormente. Se necesita una suposición para simplificar la expresión
• independencia condicional: la observación es que C es la causa directa de T y A. Una vez que sabemos que el paciente tiene C, suponemos que la probabilidad de A no depende de la presencia de T y viceversa; expresándolo matemáticamente:
  
  
  lo cual nos permite simplificar la ecuación de actualización bayesiana:
  
  • el término 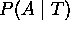parece implicar la necesidad de considerar todos los pares, triplas, etc de síntomas
  • en el denominador 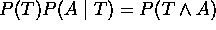puede eliminarse por normalización si suministramos 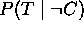y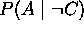
  • por tanto para la actualización bayesiana necesitaremos sólo la probabilidad a priori de la causa y las probabilidades condicionales de cada uno de sus efectos
• independencia condicional en el caso multivaluado
  • X e Y son independiente dado Z
    
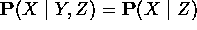
  • la regla de múltiple evidencia simplificada
    
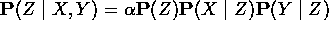
    donde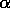 es una constante de normalización que permite que las entradas de 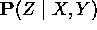sumen 1