Búsqueda

• minimiza el coste total del camino
• 
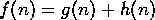
  • g(n) es el coste conocido de alcanzar el nodo n
  • h(n) es el menor coste estimado para alcanzar el objetivo
• completa y óptima si h es admisible
• optimamente eficiente entre los algoritmos óptimos
• complejidad espacial y temporal: crecimiento exponencial a no ser que el error en la función heurística crezca menos que el log del coste real
  • 
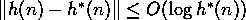
  • error al menos proporcional a la longitud del camino en la mayoría de las heurísticas
  • por tanto se espera crecimiento exponencial
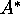  • mantiene todos los nodos en memoria. Empíricamente se queda sin memoria antes de consumir el tiempo
• heurísticas admisibles
  • h(n) nunca sobreestima el coste real
  • f(n) nunca decrece a lo largo del camino (monótona creciente)
  • si no lo fuese se podría arreglar haciendo
    • f(n')= max(f(n), g(n') + h(n')) n' nodo padre de n
  • ya que f(n) es monótona creciente puede dibujar contornos, complitud
  • IF 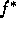es el coste de una solución óptima THEN:
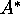    • expande todos los nodos con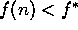
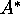    • expande algunos nodos con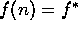
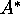    • no expande todos los nodos con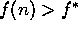
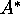    • es optimamente eficiente
  • Prueba formal de la optimalidad de
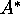
    • Sea G un estado objetivo óptimo con coste de camino 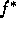, sea 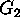un estado objetivo subóptimo 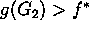. Supongamos que 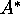ha seleccionado 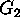, esto terminaría la búsqueda con una solución subóptima. La demostración probará que esto no es posible
    • ya que h es admisible
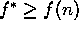
    • además si n no se ha elegido,
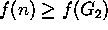
    • por tanto
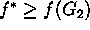
    • ya que 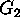es un estado objetivo, 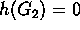, y por tanto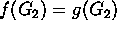
    • por tanto 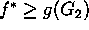, lo que contradice la suposición de que 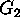es subóptimo. Esto es 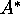nunca selecciona un estado objetivo subóptimo para expansión, por tanto es un algoritmo óptimo