Up: Indice Temas
January 21/1997

Esta es una lista de errores advertidos, correciones y ampliaciones. Deseo agradecer las sugerencias de José María Barja, Eloy J. Mata


TEMA 3
Sección: Estrategias de búsqueda... Primero en profundidad
-poner m en vez de d, m es la profundidad máxima del árbol de búsqueda.
Sección: Estrategias de búsqueda... Coste Uniforme
-poner " óptima: si, si no hay costes negativos " en vez de " completa: si, si no hay costes negativos ". Ello no implica que la primera solución encontrada sea la óptima tal y como se sigue del ejemplo de RussellyNorvig. Pero si los costes pueden ser negativos es necesaria una búsqueda exhaustiva para asegurar que esta estrategia encuentra la solución óptima.


TEMA 4
Sección:Búsqueda el primero mejor. Búsqueda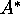
-poner "n nodo padre de n'" en vez de "n' nodo padre de n".
-poner " 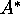no expande nodos con 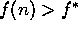" en vez de " 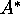no expande todos los nodos con "


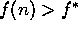TEMA 5
Sección: Representación, razonamiento y lógica.
-Sentencias válidas o necesariamente ciertas: sentencias que son ciertas bajo cualquier (todas las) interpretaciónes en todos los mundos posibles; también llamadas tautologías o sentencias analíticas
-Una sentencia es satisfacible si existe una interpretación en algún mundo posible en la que es cierta

Sección: Lógica proposicional. Sintaxis
-Poner "de mayor a menor prioridad" en lugar de "de menor a mayor prioridad"

Sección: Lógica proposicional. Semántica
-Un símbolo proposicional puede tener cualquier significado, por tanto la interpretación puede ser un hecho arbitrario cualquiera. Una sentencia que contiene un símbolo proposicional es cierta si se da el caso del hecho al que se refiere.
-La interpretación de la sentencia True es el hecho siempre verdadero, la forma en la que el mundo realmente es.
-Una traducción más adecuada del término inglés compositional language es la de lenguaje veritativo funcional.
-En la definición de modelo propuesta implícitamente se considera que la interpretación es cierta en un mundo posible. Una definición que explicite este hecho es la siguiente:
Un modelo de una sentencia bajo una determinada interpretación es un mundo en el que la sentencia es cierta bajo esa determinada interpretación.

Sección: Lógica proposicional. Inferencia en lógica proposicional. Complejidad de la ...
-"aplicar modus ponens" en lugar de "applicar modus ponens".
-Un algoritmo para la satisfacibilidad de Sentencias Horn.
En las notas se han introducido las sentencias Horn en su forma implicativa. Realmente una sentencia Horn es una sentencia en FNC (forma normal conjuntiva) con una condición adicional. Una sentencia FNC es una conjunción de sentencias, donde cada sentencia es una disyunción de literales. La condición adicional para que una sentencia FNC sea una sentencia Horn es que cada disyunción de literales contenga como máximo un literal positivo.
Supongamos que queremos establecer la satisfacibilidad de una sentencia S formada por las sentencias atómicas A1, A2, ..., An. Comenzamos escribiendo todas las sentencias en una fila seguidas por la sentencia S, como si quisiéramos construir una tabla de verdad.
Comenzamos comprobando si alguna de las sentencias atómicas es una conjunción de S. Si es así escribimos TRUE en la columna correspondiente a esa sentencia atómica. Ahora usamos esas asignaciones a TRUE para rellenar todo lo que podamos en la parte derecha de la tabla. Si por ejemplo hemos escrito TRUE debajo de A5 tendremos que escribir FALSE donde encontremos notA5. Esto puede llevarnos a rellenar más sentencias atómicas con TRUE. Por ejemplo si (A1 or notA5) es una conjunción de S, tendremos que escribir TRUE debajo de A1.
Este procedimiento finalizará de una de las formas siguientes. Podemos llegar a un punto donde asignamos FALSE a una de las conjunciones de S y por tanto a S. En este caso la sentencia S no es satisfacible. En otro caso S es satisfacible. Rellenando las columnas restantes de sentencias atómicas con FALSE tendremos una asignación de verdad que hace S cierto.
Una prueba formal de la corrección del algoritmo puede encontrarse en el capítulo 10 de J.Barwise, J. Etchemendy. The Language of First Order Logic (third edition). CSLI, Stanford, 1992.



TEMA 6
Sección: Ontología, sintaxis y semántica
-Equivalencias entre cuantificadores.
En la primera equivalencia se ha introducido un error tipográfico. Lo correcto debe ser: Ax notP es equivalente a not Ex P donde A es el cuantificador universal para todo y E es el cuantificador existencial existe.

Sección: Ejemplos de uso de la lógica de primer orden
-En el ejemplo del dominio de las relaciones familiares deben hacerse los siguientes cambios:
En la parte derecha de la equivalencia del segundo axioma debe ponerse Hombre en ver de Mujer y Esposo en vez de Esposa.
En todos los axiomas debe ponerse Padres en vez de Padre y Abuelos en vez de Abuelo. De esta forma la semántica del predicado Padres es la de la relación "ser padre o madre de" y reservamos los nombres Padre y Madre para las funciones que nombran al padre o a la madre. Ocurre lo mismo con el predicado Abuelos y las funciones Abuelo y Abuela.
-En el segundo axioma del dominio de los conjuntos falta un paréntesis derecho que cierre a la derecha toda la expresión.



TEMA 7
Sección: Completitud y decidibilidad
-Completeness y decidability son los términos ingleses. Una traducción alternativa más elegante puede ser completud y decibilidad.

Sección: Resolución ... Formas canónicas
-La resolución generalizada con disyunciones se aplica para literales, que se definen como sentencias atómicas o sentencias atómicas negadas. La resolución generalizada con implicaciones se aplica solamente a sentencias atómicas y no a literales (por lo tanto no pueden aparecer sentencias atómicas negadas).
-FNC y FNI es la traducción al español de las abreviaturas inglesas CNF e INF.
-En la definición de FNC se ha usado "gran conjunción" con un significado gráfico (el \bigwedge de LATEX). Una definición más precisa se encuentra en las correcciones al Tema 5 en esta misma página.
-FNI no es un nombre estándar. Ya en 1934 Gerhard Gentzen en sus trabajos sobre deducción natural acuñó el nombre de secuentes para las sentencias en forma normal implicativa.

Sección: Resolución ... Prueba
-A pesar de que refutación es una traducción correcta de refutation, en este ámbito una traducción mejor es la de prueba por contradicción o prueba por reducción al absurdo.

Sección: Resolución ... Conversión a forma normal
-en el paso 8 (Conversión a INF), en la disyunción de literales c y d no deben aparecer negados para que la forma implicativa normal que aparece en el ejemplo sea la que corresponde con la disyunción de literales del ejemplo

Sección: Resolución ... Teorema de la incompletud de Gõdel
-El teorema es aplicable no sólo a la aritmética sino a cualquier sistema formal equiparable (con principio de inducción matemática).



TEMA 8
Sección: Algunas cuestiones ... Diseño de la base de conocimiento
-Si la KB es una lista de conjunciones Fetch y Store son O(1) pero si se quieren evitar duplicados, Store es de O(n).
-Poner "Indexado con árboles" en lugar de "Indexado con tablas" en el tercer punto de este apartado.

Sección: Prolog y otros sistemas ... El lenguaje Prolog
-Todas las variables de Prolog están cuantificadas universalmente.
-Variables distintas en cláusulas distintas son distintas.

Sección: Probadores de teoremas. Otter
-Los hechos importantes del dominio son los hechos sobre el problema concreto.
-En lugar de "conocimiento sobre el problema" poner "conocimiento sobre el area o campo del problema background".

Sección: Sistemas de producción
-La memoria de trabajo de los sistemas de producción también suele llamarse Base de Hechos y la memoria de reglas Base de Reglas.

Sección: Sistemas de producción. Fase de emparejamiento
-Poner "la red se modifica" en lugar de "necesita modificarse a si mismo".

Sección: Redes semánticas y marcos. Herencia con excepciones
-El significado del predicado Holds es que la relación se estable explícitamente o se infiere.
-En la definición del predicado Intervening poner "x pertenece a i" en lugar de "x pertenece a p ".

Sección: Redes semánticas y marcos. Herencia y cambio
-Poner "la herencia de propiedades con excepciones es no monótona" en lugar de "la herencia de propiedades es no monótona"

Sección: Sistemas de mantenimiento de verdad.
-En el punto sobre TMS poner "suposiciones" en lugar de "supociones"

---

Alvaro Barreiro García